The Monte Carlo tuner

competition_type string: "mc_tuner".

The Monte Carlo tuner treats the tuning event as a bandit problem. That is, it attempts to find the candidate which has the highest probability of beating the opponent, and arranges to ‘spend’ more games on the candidates which have the highest winning percentages so far.

It does this using a form of the UCB algorithm (or, optionally, UCT) which is familiar to Go programmers.

Caution

As of Gomill 0.8.2, the Monte Carlo tuner is still experimental. The control file settings may change in future. The reports aren’t very good.

Page contents

The parameter model
Candidates
The tuning algorithm
Sample control file
Control file settings
Parameter configuration
Predefined scales
Writing scale functions
Reporting
Tree search
Changing the control file between runs

The parameter model

The Monte Carlo tuner expects to work with one or more independent player parameters.

Internally, it models each parameter value as a floating point number in the range 0.0 to 1.0. It uses parameter values taken uniformly from this range to make the candidate players. Values from this range are known as optimiser parameters.

In practice, engine parameters might not be floating point numbers, their range is unlikely to be 0.0 to 1.0, and you may wish to use a non-uniform (eg, logarithmic) scale for the candidates.

To support this, each parameter has an associated scale. This is a function which maps an optimiser parameter to an engine parameter (which can be of an arbitrary Python type). A number of predefined scales are provided.

The candidate players are configured using these engine parameters.

Reports, and the live display, are also based on engine parameters; see the format parameter setting.

Candidates

Each parameter also has a split setting (a smallish integer). This determines how many ‘samples’ of the parameter range are used to make candidate players.

When there are multiple parameters, one candidate is made for each combination of these samples. So if there is only one parameter, the total number of candidates is just split, and if there are multiple parameters, the total number of candidates is the product of all the split settings. For example, the sample control file below creates 64 candidates.

Caution

While the Monte Carlo tuner does not impose any limit on the number of parameters you use, unless the games are unusually rapid it may be unreasonable to try to tune more than two or three parameters at once.

Each candidate’s engine parameters are passed to the make_candidate function, which returns a Player definition.

The samples are taken by dividing the optimiser parameter range into split divisions, and taking the centre of each division as the sample (so the end points of the range are not used). For example, if a parameter has a linear scale from 0.0 to 8.0, and split is 3, the samples (after translation to engine parameters) will be 1.0, 4.0, and 7.0.

The tuning algorithm

Each time the tuner starts a new game, it chooses the candidate which gives the highest value to the following formula:

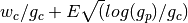
$w_c/g_c + E \sqrt(log(g_p) / g_c)$

where

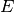$E$ is the exploration_coefficient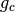
$g_c$ is the number of games the candidate has played
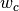$w_c$ is the number of games the candidate has won
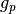$g_p$ is the total number of games played in the tuning event

At the start of the tuning event, each candidate’s 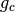$g_c$ is set to initial_visits, and 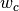$w_c$ is set to initial_wins.

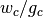( $w_c/g_c$ is just the candidate’s current win rate. 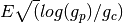$E \sqrt(log(g_p) / g_c)$ is known as the exploration term; as more games are played, its value increases most rapidly for the least used candidates, so that unpromising candidates will eventually be reconsidered.)

When more than one candidate has the highest value (for example, at the start of the event), one is chosen at random.

The tuning event runs until number_of_games games have been played (indefinitely, if number_of_games is unset).

The tuner can be stopped at any time; after each game result, it reports the parameters of the current ‘best’ candidate. This is the candidate with the most wins (note that this may not be the one with the best win rate; it is usually the same as the candidate which has played the most games).

Sample control file

Here is a sample control file, illustrating most of the available settings for a Monte Carlo tuning event:

competition_type = "mc_tuner"

description = """\
This is a sample control file.

It illustrates the available settings for the Monte Carlo tuner.
"""

players = {
    'gnugo-l10' : Player("gnugo --mode=gtp --chinese-rules "
                         "--capture-all-dead --level=10"),
    }

def fuego(max_games, additional_commands=[]):
    commands = [
        "go_param timelimit 999999",
        "uct_max_memory 350000000",
        "uct_param_search number_threads 1",
        "uct_param_player reuse_subtree 0",
        "uct_param_player ponder 0",
        "uct_param_player max_games %d" % max_games,
        ]
    return Player(
        "fuego --quiet",
        startup_gtp_commands=commands+additional_commands)

FUEGO_MAX_GAMES = 5000

parameters = [
    Parameter('rave_weight_initial',
              scale = LOG(0.01, 5.0),
              split = 8,
              format = "I: %4.2f"),

    Parameter('rave_weight_final',
              scale = LOG(1e2, 1e5),
              split = 8,
              format = "F: %4.2f"),
    ]

def make_candidate(rwi, rwf):
    return fuego(
        FUEGO_MAX_GAMES,
        ["uct_param_search rave_weight_initial %f" % rwi,
         "uct_param_search rave_weight_final %f" % rwf])

board_size = 19
komi = 7.5
opponent = 'gnugo-l10'
candidate_colour = 'w'
number_of_games = 10000

exploration_coefficient = 0.45
initial_visits = 10
initial_wins = 5

summary_spec = [40]
log_tree_to_history_period = 200

Control file settings

The following settings can be set at the top level of the control file:

All common settings (the players dictionary is required, though it is used only to define the opponent).

The following game settings (only board_size and komi are required):

komi must be fractional, as the tuning algorithm doesn’t currently support jigos.

The following additional settings (all those without a listed default are required):

number_of_games

Integer (default None)

The total number of games to play in the event. If you leave this unset, there will be no limit.

candidate_colour

String: "b", "w", or "random"

The colour for the candidates to take in every game.

opponent

Identifier

The player code of the player to use as the candidates’ opponent.

parameters

List of Parameter definitions (see Parameter configuration).

Describes the parameter space that the tuner will work in. See The parameter model for more details.

The order of the Parameter definitions is used for the arguments to make_candidate, and whenever parameters are described in reports or game records.

make_candidate

Python function

Function to create a Player from its engine parameters.

This function is passed one argument for each candidate parameter, and must return a Player definition. Each argument is the output of the corresponding Parameter‘s scale.

The function will typically use its arguments to construct command line options or GTP commands for the player. For example:

def make_candidate(param1, param2):
    return Player(["goplayer", "--param1", str(param1),
                   "--param2", str(param2)])

def make_candidate(param1, param2):
    return Player("goplayer", startup_gtp_commands=[
                   ["param1", str(param1)],
                   ["param2", str(param2)],
                  ])

exploration_coefficient

Float

The coefficient of the exploration term in the UCB algorithm (eg 0.45). See The tuning algorithm.

initial_visits

Positive integer

The number of games to initialise each candidate with. At the start of the event, the tuner will behave as if each candidate has already played this many games. See The tuning algorithm.

initial_wins

Positive integer

The number of wins to initialise each candidate with. At the start of the event, the tuner will behave as if each candidate has already won this many games. See The tuning algorithm.

Tip

It’s best to set initial_wins so that initial_wins / initial_visits is close to the typical candidate’s expected win rate.

max_depth

Positive integer (default 1)

See Tree search below.

The remaining settings only affect reporting and logging; they have no effect on the tuning algorithm.

summary_spec

List of integers (default [30])

Number of candidates to describe in the runtime display and reports (the candidates with most visits are described).

(This list should have max_depth elements; if max_depth is greater than 1, it specifies how many candidates to show from each level of the tree, starting with the highest.)

log_tree_to_history_period

Positive integer (default None)

If this is set, a detailed description of the UCT tree is written to the history file periodically (after every log_tree_to_history_period games).

number_of_running_simulations_to_show

Positive integer (default 12)

The maximum number of games in progress to describe on the runtime display.

Parameter configuration

A Parameter definition has the same syntax as a Python function call: Parameter(arguments). Apart from code, the arguments should be specified using keyword form (see Sample control file).

All arguments other than format are required.

The arguments are:

code

Identifier

A short string used to identify the parameter. This is used in error messages, and in the default for format.

scale

Python function

Function mapping an optimiser parameter to an engine parameter; see The parameter model.

Although this can be defined explicitly, in most cases you should be able to use one of the predefined scales.

Examples:

Parameter('p1', split = 8,
          scale = LINEAR(-1.0, 1.0))

Parameter('p2', split = 8,
          scale = LOG(10, 10000, integer=True))

Parameter('p3', split = 3,
          scale = EXPLICIT(['low', 'medium', 'high']))

def scale_p3(f):
    return int(1000 * math.sqrt(f))
Parameter('p3', split = 20, scale = scale_p3)

split

Positive integer

The number of samples from this parameter to use to make candidates. See The tuning algorithm.

format

String (default "parameter_code: %s")

Format string used to display the parameter value. This should include a short abbreviation to indicate which parameter is being displayed, and also contain %s, which will be replaced with the engine parameter value.

You can use any Python conversion specifier instead of %s. For example, %.2f will format a floating point number to two decimal places. %s should be safe to use for all types of value. See string formatting operations for details.

Format strings should be kept short, as screen space is limited.

Examples:

Parameter('parameter_1', split = 8,
          scale = LINEAR(-1.0, 1.0),
          format = "p1: %.2f")

Parameter('parameter_2', split = 8,
          scale = LOG(10, 10000, integer=True),
          format = "p2: %d")

Parameter('parameter_3', split = 3,
          scale = EXPLICIT(['low', 'medium', 'high']),
          format = "p3: %s")

Predefined scales

There are three kinds of predefined scale which you can use in a scale definition:

LINEAR

A linear scale between specified bounds. This takes two arguments: lower_bound and upper_bound.

Optionally, you can also pass integer=True, in which case the result is rounded to the nearest integer.

Examples:

LINEAR(0, 100)
LINEAR(-64.0, 256.0, integer=True)

Tip

To make candidates which take each value from a simple integer range from (say) 0 to 10 inclusive, use:

Parameter('p1', split = 11,
          scale = LINEAR(-0.5, 10.5, integer=True))

(or use EXPLICIT)

LOG

A ‘logarithmic scale’ (ie, an exponential function) between specified bounds. This takes two arguments: lower_bound and upper_bound.

Optionally, you can also pass integer=True, in which case the result is rounded to the nearest integer.

Example:

LOG(0.01, 1000)
LOG(1e2, 1e9, integer=True)

EXPLICIT

This scale makes the engine parameters take values from an explicitly specified list. You should normally use this with split equal to the length of the list.

Examples:

EXPLICIT([0, 1, 2, 4, 6, 8, 10, 15, 20])
EXPLICIT(['low', 'medium', 'high'])

Note

if max_depth is greater than 1, split ^ max_depth should equal the length of the list.

Writing scale functions

The following built-in Python functions might be useful: abs(), min(), max(), round().

More functions are available from the math module. Put a line like

from math import log, exp, sqrt

in the control file to use them.

Dividing two integers with / gives a floating point number (that is, ‘Future division’ is in effect).

You can use scientific notation like 1.3e-2 to specify floating point numbers.

Here are scale functions equivalent to LINEAR(3, 3000) and LOG(3, 3000):

def scale_linear(f):
    return 2997 * f + 3

def scale_log(f):
    return exp(log(1000) * f) * 3

Reporting

Currently, there aren’t any sophisticated reports.

The standard report shows the candidates which have played most games; the summary_spec setting defines how many to show.

In a line like:

(0,1) I: 0.01; F: 365.17                       0.537  70

The (0,1) are the ‘coordinates’ of the candidate, I: 0.01; F: 365.17 are the engine parameters (identified using the format setting), 0.537 is the win rate (including the initial_wins and initial_visits), and 70 is the number of games (excluding the initial_visits).

Also, after every log_tree_to_history_period games, the status of all candidates is written to the history file (if max_depth > 1, the first two generations of candidates are written).

Tree search

As a further (and even more experimental) refinement, it’s possible to arrange the candidates in the form of a tree and use the UCT algorithm instead of plain UCB. To do this, set the max_depth setting to a value greater than 1.

Initially, this behaves as described in The tuning algorithm. But whenever a candidate is chosen for the second time, it is expanded: a new generation of candidates is created and placed as that candidate’s children in a tree structure.

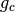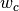The new candidates are created by sampling their parent’s ‘division’ of optimiser parameter space in the same way as the full space was sampled to make the first-generation candidates (so the number of children is again the product of the split settings). Their $g_c$ and $w_c$ values are initialised to initial_visits and initial_wins as usual.

Then one of these child candidates is selected using the usual formula, where

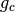$g_c$ is now the number of games the child has played
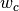$w_c$ is now the number of games the child has won
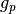$g_p$ is now the number of games the parent has played

If max_depth is greater than 2, then when a second-generation candidate is chosen for the second time, it is expanded itself, and so on until max_depth is reached.

Each time the tuner starts a new game, it walks down the tree using this formula to choose a child node at each level, until it reaches a ‘leaf’ node.

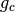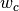Once a candidate has been expanded, it does not play any further games; only candidates which are ‘leaf’ nodes of the tree are used as players. The $g_c$ and $w_c$ values for non-leaf candidates count the games and wins played by the candidate’s descendants, as well as by the candidate itself.

The ‘best’ candidate is determined by walking down the tree and choosing the child with the most wins at each step (which may not end up with the leaf candidate with the most wins in the entire tree).

Note

It isn’t clear that using UCT for a continuous parameter space like this is a wise (or valid) thing to do. I suspect it needs some form of RAVE to perform well.

Caution

If you use a high --parallel value, note that the Monte Carlo tuner doesn’t currently take any action to prevent the same unpromising branch of the tree being explored by multiple processes simultaneously, which might lead to odd results (particularly if you stop the competition and restart it).

Changing the control file between runs

In general, you shouldn’t change the Parameter definitions or the settings which control the tuning algorithm between runs. The ringmaster will normally notice and refuse to start, but it’s possible to fool it and so get meaningless results.

Changing the exploration_coefficient is ok. Increasing max_depth is ok (decreasing it is ok too, but it won’t stop the tuner exploring parts of the tree that it has already expanded).

Changing make_candidate is ok, though if this affects player behaviour it will probably be unhelpful.

Changing initial_wins or initial_visits will have no effect if max_depth is 1; otherwise it will affect only candidates created in future.

Changing the settings which control reporting, including format, is ok.

Changing number_of_games is ok.

The Monte Carlo tuner

The parameter model

Candidates

The tuning algorithm

Sample control file

Control file settings

Parameter configuration

Predefined scales

Writing scale functions

Reporting

Tree search

Changing the control file between runs

Table Of Contents

Previous topic

Next topic